COMBINATOIRE (ANALYSE)

COMBINATOIRE (ANALYSE)

L’analyse combinatoire est l’ensemble des techniques qui servent, en mathématiques, à compter (ou dénombrer ) certaines structures finies , ou à les énumérer (établir des listes exhaustives de structures considérées), enfin à démontrer leur existence pour certaines valeurs des paramètres dont elles dépendent. Ces structures sont très variées; leur seul trait commun c’est d’être finies . En revanche, les problèmes qu’on se pose sur ces structures sont très divers, et les techniques mathématiques qu’on utilise pour résoudre ces problèmes, très différentes. Par exemple, si on veut dénombrer les arbres de n sommets, on établit une correspondance biunivoque entre l’ensemble de ces arbres et l’ensemble de certaines suites qu’on sait compter. Mais, si l’on veut démontrer l’existence d’une famille infinie de codes correcteurs, on utilise des résultats fins sur les anneaux de polynômes à coefficients dans un corps fini. Pourtant, dans les deux cas, on dit qu’on s’occupe d’analyse combinatoire. Dans le foisonnement des sujets dits de nature combinatoire, on a donc dû faire un choix et laisser de côté des objets importants.

1. Dénombrements élémentaires

Dans les opérations élementaires de dénombrement, on utilise un langage très proche du réel. On parle de choisir un objet de m façons différentes , on dit qu’il n’y a qu’un nombre n de possibilités... Considérons ainsi l’exemple suivant. Une urne contient 10 boules numérotées de 1 à 10; on tire successivement deux boules de l’urne sans remettre la première après tirage. Combien y a-t-il de tirages croissants , c’est-à-dire de façons de tirer deux boules dont les numéros vont en croissant? Pour déterminer ce nombre, on raisonne de la façon suivante. Si la première boule a été tirée et que son numéro est i (1 諒 i 諒 10), pour obtenir un tirage croissant, on peut choisir le numéro j de la seconde de 10 漣 i façons différentes. Enfin, pour obtenir un tirage croissant, on peut choisir soit un tirage commençant par le numéro 1, soit un tirage commençant par 2, etc. Le nombre de tirages croissants est alors égal à (10 漣 1) + (10 漣 2) + ... + (10 漣 9) + (10 漣 10) = 45. On a implicitement utilisé les deux règles suivantes (la seconde avant la première):

– Règle de la somme : Si on peut choisir un objet a de m façons et un objet b de n façons, on peut choisir a ou b de m + n façons.

– Règle du produit : Si on peut choisir un objet a de m façons, puis un objet b de n façons, on peut choisir a puis b , dans cet ordre , de mn façons.

Reprenons l’exemple ci-dessus. Pour caractériser un tirage, il suffit de se donner un couple (i , j ) d’entiers tels que i et j soient compris entre 1 et 10. Désignons par X l’ensemble des couples (i , j ) tels que 1 諒 i 麗 j 諒 10. Les tirages croissants correspondent aux éléments de X et, pour trouver le nombre de tirages croissants, il suffit de dénombrer l’ensemble X, c’est-à-dire de compter le nombre de ses éléments. Pour 1 諒 h 諒 10, notons X^h l’ensemble des couples (i , j ) de X tels que i = h ; ainsi X^h est le produit cartésien des ensemblesh eth + 1, h + 2, ..., 10. De plus, les ensembles X^h sont disjoints deux à deux et leur réunion est X. Désignons par |X^h | le nombre des éléments de X^h ; alors en posant k = 10, le nombre, noté |X| des éléments de X est donné par:

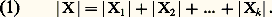De plus, pour 1 諒 h 諒 10, on a:

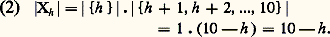En appliquant les formules (1) et (2), on retrouve bien 45 pour le nombre des éléments de X. Dans cette dernière démarche, nous avons résolument adopté le langage de la théorie des ensembles et utilisé certains résultats sur les ensembles finis . D’abord comment caractérise-t-on les ensembles finis? En premier lieu, on définit une numérotation d’un ensemble X comme une suite x ¹, x ², ..., x ⁿ d’éléments de X telle x ⁱ x ^j pour i j et telle que tout élément de X soit l’un des x ⁱ . Les ensembles finis sont ceux qui possèdent une numérotation. L’entier n qui apparaît dans une numérotation d’un ensemble fini X s’appelle le cardinal de X ou le nombre d’éléments de X et se note |X|. Cet entier ne dépend pas en effet de la numérotation choisie. On convient que | 歷| = 0. On obtient alors:

– Formule de la somme : Si X et Y sont deux ensembles finis, disjoints , l’ensemble X 聆 Y est fini et l’on a:

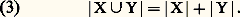– Formule du produit : Si X et Y sont deux ensembles finis, le produit cartésien X 憐 Y de X par Y est fini et l’on a:

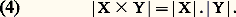Ces deux formules se démontrent de la même façon. On détermine une numérotation de X 聆 Y et de X 憐 Y, supposant données des numérotations de X et de Y et on vérifie les formules (3) et (4).

Ces formules ont été utilisées, de façon explicite, dans l’exemple, en (1) et (2). Elles sont la traduction dans le langage de la théorie des ensembles des règles de la somme et du produit. On ne parle plus de «choisir un objet a de m façons», mais on considère l’ensemble X des choix possibles pour a et l’on suppose que l’on a |X| = m . Cette transcription nous permettra dans la suite d’utiliser indifféremment les deux langages. Lorsque les ensembles X et Y sont des ensembles finis quelconques, on peut exprimer les ensembles X 聆 Y et Y comme des réunions de deux ensembles disjoints, à savoir:

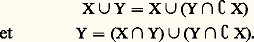En appliquant la formule de la somme dans les deux cas, on obtienta :

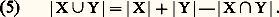Rappelons enfin un principe fondamental dans le dénombrement:

(6) Pour que deux ensembles finis X et Y aient le même cardinal, il faut et il suffit qu’il existe une bijection de X sur Y.

Dans de nombreux cas, la difficulté sera effectivement de construire une telle bijection. Examinons maintenant quelques dénombrements fondamentaux.

D’abord les trois formules (3), (4) et (5) s’étendent au cas général de k ensembles (k 閭 2). On obtient:

si Xⁱ 惡 X^j = 歷, pour i j .

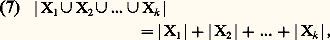De même, on a toujours:

Quant à la formule (5), sa généralisation est la suivante: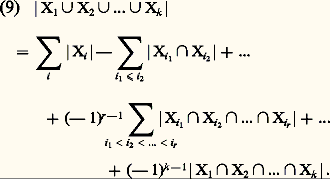

La formule (9) peut s’établir aisément par récurrence sur k . On l’appelle la formule du principe d’inclusion et d’exclusion. Elle a reçu de nombreuses applications.

Si, dans la formule (8), on prend tous les ensembles Xⁱ égaux au même ensemble X, on a alors:

Ainsi, l’ensemble X^k de tous les k -uples (x ¹, x ², ..., x ^k ), où les x ⁱ sont pris dans X, a pour cardinal |X|^k . Dans la littérature classique, si |X| = n , un k -uple (x ¹, x ², ..., x ^k ) était appelé arrangement avec répétition de n objets pris k à k .

Soit maintenant y ¹, y ², ..., y ^k une numérotation d’un ensemble fini Y. Pour définir une application f de Y dans X, il suffit de se donner arbitrairement des éléments x ¹, x ², ..., x ^k (non nécessairement distincts) de X et de poser f (y ⁱ ) = x ⁱ pour 1 諒 i 諒 k . On définit ainsi une bijection de l’ensemble X^k des k -uples (x ¹, x ², ..., x ^k ) pris dans X sur l’ensemble, noté X^Y, de toutes les applications de Y dans X. La formule (10) et le principe (6) impliquent donc:

D’autre part, l’application qui fait correspondre à toute partie A de X sa fonction caractéristique 﨏^A est une bijection de l’ensemble, noté 戮(X), de toutes les parties de X sur l’ensemble0, 1^X des applications de X dans0, 1. La formule précédente implique alors | 戮(X)| = |0, 1^|X| = 2^|X|. Soit

Dénombrement des injections

Considérons deux ensembles finis X et Y avec |X| = n , |Y| = p et n 諒 p . Soit 琉 l’ensemble des injections de X dans Y, c’est-à-dire des applications f de X dans Y telles que les relations x , x 捻 X, x x entraînent f (x ) f (x ). Il est clair que | 琉| ne dépend que de p et de n ; posons | 琉| = A(p , n ). Prenons un ensemble X disjoint de X avec |X | = p 漣 n . L’ensemble X = X 聆 X a ainsi p éléments. Pour définir une bijection de X sur Y, il suffit de se donner une injection f de X dans Y et une bijection g de X sur Y 漣 f (X). On peut choisir f de A(p , n ) façons, puis g de A(p 漣 n , p 漣 n ) façons. La règle du produit permet ainsi d’écrire: A(p , p ) = A(p , n ) A (p 漣 n , p 漣 n ), où 0 諒 n 諒 p . Comme on a: A(p , 1) = p et A(p , 0) = 1 (en convenant qu’il y a une application d’un ensemble vide dans tout ensemble), il vient: A(p, p ) = p A(p 漣 1, p 漣 1). D’où A(p , p ) = p !, en posant 0! = 1 et p ! = p (p 漣 1)! pour p 閭 1. On a enfin: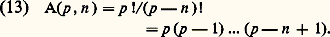

Soit x ¹, x ², ..., x ⁿ une numérotation donnée de X; pour définir une injection f de X dans Y, il suffit encore de se donner arbitrairement une suite de n éléments (y ¹, y ², ..., y ⁿ ) de Y tous distincts et de poser f (x ⁱ ) = y ⁱ pour 1 諒 i 諒 n . On trouve ainsi que le nombre de n -uples (y ¹, y ², ..., y ⁿ ), où les yⁱ sont des éléments tous distincts, pris dans un ensemble Y de cardinal p , est égal à p !/(p 漣 n )!. Dans les ouvrages classiques, un tel n -uple est appelé arrangement sans répétition de p objets pris n à n .

Si on prend Y = X, la formule (13) implique que le nombre de bijections de X sur lui-même – on dit aussi permutations de X – est égal à n !.

Soit C^{n p} le nombre de parties de Y qui ont n éléments. Pour définir une injection de X dans Y, il suffit de se donner une partie A de Y ayant n éléments, puis une bijection f de X sur A. On peut choisir A de C^{n p} façons, puis f de n ! façons. On a donc | 琉| = C^{n p} n !. D’où C^{n p} = A(p, n )/n ! = p !/(n !(p 漣 n )!). Les nombres C^{n p} sont les coefficients binominaux : C^{n p} est aussi noté fréquemment: (pn ). Ce sont eux qui apparaissent dans la formule dite du binôme :

valable dans tout anneau commutatif. Notons que l’on a: C^0p = C^{p p} = 1, C^1p = p , C^{n p} = C^{p p-n} . On vérifie également la propriété C^{n p} = C^{n p-1} + C^{n-1 p-1} , qui permet de les déterminer de proche en proche. Le coefficient C^{n p} est aussi le nombre des combinaisons de p éléments pris n à n , mais on tend à abandonner cette terminologie, une combinaison n’étant qu’un sous-ensemble A, de cardinal n , d’un ensemble Y de cardinal p .

Dénombrement des applications croissantes de X dans Y

Supposons que l’on prenne pour les ensembles X et Y X =1, 2, ..., n et Y =1, 2, ..., p, où les entiers n et p sont quelconques. Une application f de X dans Y est dite croissante si l’on a f (i ) 諒 f (j ) pour tout couple (i , j ) tel que 1 諒 i 諒 j 諒 n . Par un raisonnement déjà utilisé plus haut, on vérifie que l’ensemble 臨 de toutes les applications croissantes de X dans Y a même cardinal que l’ensemble 臨 des suites croissantes (y ¹, y ², ..., y ⁿ ) de n termes pris dans Y, c’est-à-dire qui satisfont à y ¹ 諒 y ² 諒... 諒 y ⁿ . Une telle suite est encore appelée combinaison avec répétition de p objets pris n à n. À son tour, 臨 a même cardinal que l’ensemble 臨 des suites (z ¹, z ², ...., z ⁿ ) de n termes où les z ⁱ sont pris dans l’ensemble1, 2, ..., p + n 漣 1 et satisfont à z ¹ 麗 z ² 麗 ... 麗 z ⁿ . On établit en effet une bijection de 臨 sur 臨 en faisant correspondre à la suite (y ¹, y ², ..., y ⁿ ) de 臨 la suite (y ¹ + 0, y ² + 1, ..., y ⁿ + n 漣 1). On a ainsi | 臨| = | 臨 | = C^{n p+n-1} .

Dénombrement des surjections

Soit X et Y deux ensembles finis, respectivement de cardinal n et p . Désignons par 崙 l’ensemble des surjections de X sur Y, c’est-à-dire des applications f de X dans Y, telles que pour tout y 捻 Y, il existe un x 捻 X satisfaisant à f (x ) = y . L’ensemble 崙 est vide si n 麗 p. Supposons désormais que l’on a n 閭 p . On ne connaît pas de formule explicite donnant le cardinal de 崙 en fonction de n et p . Toutefois, il existe une formule de récurrence, qui permet de le calculer de proche en proche. On appelle d’abord partition de l’ensemble X la donnée de r sous-ensembles A¹, A², ..., A^r (r 礪 0) de X (dont certains peuvent être vides) satisfaisant à Aⁱ 惡 A^j = 歷 si i j et X = A¹ 聆 A² 聆 ... 聆 A^r . Notons que pour définir une partition, on ne s’impose pas un ordre sur les Aⁱ . Désignons par S^{p n} le nombre de partitions de X en p sous-ensembles non vides. Pour définir ensuite une surjection f de X sur Y, il suffit de se donner une partition de X en p sous-ensembles non vides, puis une bijection de l’ensemble formé par ces p sous-ensembles, sur Y. D’après la règle du produit, on a | 崙| = S^{p n} p !. Il est maintenant facile de vérifier que les nombres S^{p n} satisfont aux relations de récurrence suivantes:

pour 1 麗 p 麗 n .

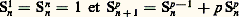Ces relations de récurrence permettent donc de calculer | 崙| de proche en proche. Les coefficients S^{p n} s’appellent les nombres de Stirling (de deuxième espèce). Donnons le tableau des premiers coefficients S^{p n} :

Par exemple, le nombre de surjections d’un ensemble de 5 éléments sur un ensemble de 3 éléments est égal à S³⁵ 3! = 150.

2. Fonctions génératrices

On a vu qu’on ne savait pas trouver de formule explicite donnant le nombre de surjections d’un ensemble de n éléments sur un ensemble de p éléments, mais on peut faire apparaître ces nombres comme coefficients d’une série. La fonction de deux variables f (t , u ) = exp (t (exp u 漣 1)) se développe en série sous la forme:

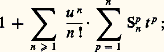le nombre de Stirling S^{p n} apparaît, divisé par n !, comme coefficient du monôme u ⁿ t ^p . On dit que la fonction f (t , u ) est la fonction génératrice des nombres S^{p n} /n !; puisqu’on connaît l’expression de cette fonction génératrice, on pourra résoudre d’autres problèmes combinatoires ou trouver des fonctions génératrices d’autres nombres liés aux nombres de Stirling.

Supposons donné un anneau A commutatif et ayant un élément unité. On appelle série formelle à coefficients dans A et en une indéterminée u , une somme symbolique infinie:

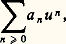où les a ⁿ sont dans A (n 閭 0). On dit que a ⁿ est le coefficient de u ⁿ dans cette série. La somme et le produit de deux séries formelles sont définis de manière à respecter les règles usuelles de distributivité pour le produit de deux séries infinies et le calcul sur les puissances u ⁿ u ^m = u ^n+m (cf. ANNEAUX ET ALGÈBRES, chap. 2): si on a deux séries:

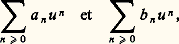leur somme est la série:

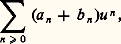et leur produit est donné par:

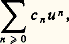où l’on a: c ⁿ = a ⁰b ⁿ + a ¹b ^n-1 +...+ a ⁿ b ⁰ pour tout n 閭 0. Si U est une telle série sans terme constant, c’est-à-dire telle que le coefficient de u ⁰ soit nul, on appelle exponentielle de U la série:

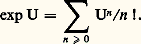En d’autres termes, exp U est la série formelle dont le coefficient de u ⁿ est le coefficient de u ⁿ dans la somme (finie):

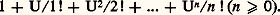Une suite infinie d’indéterminées t = (t ¹, t ², ...) étant donnée, nous prenons pour anneau A l’anneau des polynômes à coefficients rationnels dont les indéterminées sont prises dans la suite t. Posons alors:

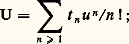son terme constant est nul, on peut donc prendre son exponentielle, qu’on peut écrire:

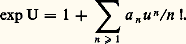Il est facile de voir que a ⁿ est un polynôme de degré n en les n variables t ¹, t ², ..., t ⁿ , où n 閭 1. Plus précisément, on a:

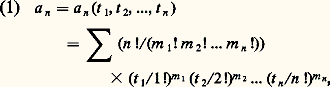où la sommation est étendue à toutes les suites (m ¹, m ², ..., m ⁿ ) de n entiers positifs satisfaisant à 1m ¹ + 2m ² + ... + nm ⁿ = n . Le coefficient du monôme:

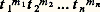dans a est donc égal à:

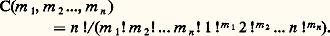On peut vérifier que ce nombre est le nombre de partitions de type (m ¹, m ², ..., m ⁿ ), c’est-à-dire de partitions de l’ensemble X =1, 2, ..., n en m ¹ + m ² + ... + m ⁿ sous-ensembles non vides, parmi lesquels m ¹ sont de cardinal 1, m ² de cardinal 2, ..., m ⁿ de cardinal n .

Cette interprétation nous permet de retrouver le nombre de partitions de l’ensemble X =1, 2, ..., n en p sous-ensembles non vides. En effet, le nombre de sous-ensembles non vides d’une partition de type (m ¹, m ², ..., m ⁿ ) est p = m ¹ + m ² + ... + m ⁿ . Si donc l’on pose t ¹ = t ² = ... = t ⁿ = t dans l’expression (1), le coefficient de t ^p dans le second membre va être égal au nombre de partitions de X en p sous-ensembles non vides, soit:

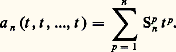Par conséquent la fonction génératrice des nombres de Stirling de seconde espèce est donnée par:

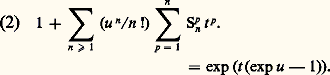Par exemple, pour trouver le nombre de surjections d’un ensemble de n éléments sur un ensemble de p éléments (p 諒 n ), on détermine le coefficient c de u ⁿ t ^p dans le développement de exp (t (exp u 漣 1)) et le nombre cherché est égal à cn ! p !.

3. Construction de correspondances

Dans la première partie, nous avons passé en revue tous les ensembles finis qu’il était aisé de dénombrer en faisant usage des deux règles de la somme et du produit. Ces techniques élémentaires s’appliquent plus difficilement lorsqu’on veut dénombrer d’autres structures finies plus élaborées comme celles des arbres ou certains types de graphes . Le plus souvent on est conduit à chercher une correspondance biunivoque entre ces structures et les ensembles finis considérés dans la première partie. Jusqu’ici, il n’existe pas de théorie pour construire ces correspondances, tout est une question d’ingéniosité et de patience. À titre d’exemple, on peut décrire ci-dessous une telle correspondance entre les arbres de n sommets et les (n 漣 2)-uples (x ¹, x ², ..., x ^n-2 ), où les x ⁱ sont des entiers compris entre 1 et n .

Un graphe est la donnée d’un ensemble X – ses éléments sont les sommets du graphe – et d’une classe U de sous-ensembles de X à deux éléments, appelés arêtes . Si l’on a x , y 捻 X etx , y 捻 U, on dit que x et y sont adjacents. Une chaîne du grapheX, U est une suitex ¹, y ¹,x ², y ², ...,x ⁿ , y ⁿ d’arêtes distinctes telle que, lorsque n 礪 1, on ait: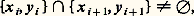

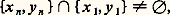pour i = 1, 2, ..., n 漣 1. Si de plus, on a n 礪 1 et

on dit que la chaîne est un cycle . Un graphe est dit connexe si, pour tout couple de sommets distincts (x , y), il existe une chaînex ¹, y ¹,x ², y ², ...,x ⁿ , y ⁿ telle que x ¹ = x et y ⁿ = y . Un arbre de n sommets est alors défini comme un graphe de n sommets qui est connexe et sans cycles. On a l’habitude de représenter un graphe fini de n sommets comme un ensemble de n points du plan numérotés de 1 à n où les sommets i et j sont reliés entre eux si et seulement si l’on ai , j 捻 U. Considérons par exemple le graphe de la figure ci-dessus. C’est un arbre de sept sommets, numérotés de 1 à 7.

Soit Aⁿ l’ensemble de tous les arbres possibles de n sommets numérotés 1, 2, ..., n . Cayley fut le premier à démontrer que l’on a |Aⁿ | = n ^n-2 . Or ce nombre est précisément le cardinal de l’ensemble Hⁿ de tous les (n 漣 2)-uples (x ¹, x ², ..., x ^n-2 ) où les x ⁱ sont pris dans X =1, 2, ..., n (formule (11) de la première partie). Pour démontrer la formule |Aⁿ | = n ^n-2 , il suffit donc de construire une bijection 淋 de Aⁿ sur Hⁿ . Nous donnons ici la construction d’une telle correspondance due à Prüfer. Celle-ci fait usage des deux propriétés suivantes sur les arbres, faciles à vérifier. D’abord, un arbre a toujours (au moins) un sommet pendant , c’est-à-dire un sommet qui n’est adjacent qu’à un seul autre sommet. Ensuite, si l’on «efface» un sommet pendant d’un arbre de n sommets, et l’arête qui le contient, on obtient un arbre de (n 漣 1) sommets. La construction de Prüfer est alors la suivante: pour un arbre de Aⁿ donné, on efface le plus petit sommet pendant et l’on désigne par x ¹ l’unique sommet qui était adjacent à ce sommet pendant. On répète cette opération avec l’arbre restant de (n 漣 1) sommets et l’on détermine x ² et ainsi de suite. On s’arrête lorsqu’il ne reste plus que deux sommets (adjacents). Par exemple, à l’arbre de la figure 1 on fait correspondre la suite (1, 7, 1, 7, 7). Les sommets pendants qu’on a successivement effacés sont 2, 3, 4, 1, 5 et il est resté l’arbre formé par les deux sommets 6 et 7. On vérifie que l’application 淋 de Aⁿ sur Hⁿ ainsi construite est bien bijective. D’où l’on déduit |Aⁿ | = |Hⁿ | = n ^n-2 .

4. Théorèmes d’existence

Le théorème de Ramsey et celui de Hall-König, dont nous donnons les énoncés maintenant, jouent un rôle spécial en combinatoire. Ils assurent l’existence de certaines configurations dans des conditions très générales et ont ainsi trouvé de nombreuses applications.

Supposons que l’on ait un graphe de six sommets, dans lequel deux sommets distincts sont joints par une arête «coloriée» en bleu ou en rouge. Démontrons la propriété (P) suivante: Il existe un triangle dont les trois arêtes ont la même couleur. Considérons en effet les cinq arêtes issues d’un sommet donné S¹ du graphe. Nécessairement trois de ces arêtes ont la même couleur, disons bleue; appelons-les S¹S², S¹S³ et S¹S⁴. Si l’une des arêtes S²S³, S²S⁴, S³S⁴ est bleue, disons S²S³, le triangle S¹S²S³ est bleu. Sinon les arêtes S²S³, S²S⁴, S³S⁴ sont rouges, mais alors le triangle S²S³S⁴ est rouge. La propriété (P) est ainsi vérifiée. L’argument essentiel qui a été utilisé est le principe des tiroirs : si l’on met n objets dans p tiroirs (p 諒 n ), alors le nombre des objets dans au moins un tiroir est supérieur ou égal à n /p . Le théorème de Ramsey peut être considéré comme une généralisation de ce principe.

Théorème de Ramsey . Soit X un ensemble de n éléments et supposons donnés d’abord trois entiers p , q , r satisfaisant à p 閭 r , q 閭 r et r 閭 1, ensuite une partition de l’ensemble de toutes les parties de X de cardinal r , en deux classes 戮 et 隆 陸. Alors il existe un entier N(p , q , r ) ne dépendant que des entiers p , q , r et non pas de l’ensemble X tel que la propriété (P ) suivante soit vérifiée: Si n 閭 N(p , q , r ), il existe ou bien une partie A de X de p éléments qui a tous ses sous-ensembles de cardinal r dans 戮, ou bien une partie B de q éléments qui a tous ses sous-ensembles de cardinal r dans 隆 陸.

Dans l’exemple précédent, on avait n = 6, p = q = 3 et r = 2. Les ensembles de deux éléments sont alors les arêtes, qui sont divisées en deux classes, les bleues (classe 戮) et les rouges (classe 隆 陸). La propriété (P) équivaut à dire que l’on a N(3, 3, 2) 閭 6. En fait, on a l’égalité.

Le théorème de Hall-König peut être énoncé de deux façons différentes, soit en termes de systèmes de représentants distincts, soit en termes de matrices à coefficients 0 ou 1. Nous ne donnerons pas ici l’énoncé sous cette dernière forme. Soit X =1, 2, 3, 4, 5 l’ensemble des cinq premiers entiers et considérons les sous-ensembles X¹ =1, 4, X² =1, 2, 4, X³ =1, 2, 4 et X⁴ =2, 4, 5 de X. On peut choisir des entiers x ¹, x ², x ³, x ⁴ de sorte que l’on ait x ⁱ 捻 Xⁱ pour 1 諒 i 諒 4 et que tous les x ⁱ soient distincts . Il suffit de prendre en effet les nombres x ¹ = 1, x ² = 2, x ³ = 4, x ⁴ = 5. Si on remplace dans cet exemple X⁴ par X⁴ =2, 4, un tel choix n’est plus possible puisque la réunion des quatre ensembles X¹, X², X³, X⁴ ne contient que trois éléments distincts 1, 2, 4. On est ainsi amené à donner la définition suivante: Étant donné une suite (X¹, X², ..., Xⁿ ) de parties d’un ensemble non vide X, on dit que cette suite possède un système de représentants distincts , s’il existe une suite (x ¹, x ², ..., x ⁿ ) de n éléments distincts de X satisfaisant à x ⁱ 捻 Xⁱ pour tout i tel que 1 諒 i 諒 n.

Théorème de Hall-König. La condition nécessaire et suffisante pour qu’une suite (X¹, X², ..., Xⁿ ) de parties d’un ensemble non vide X possède un système de représentants distincts est que, pour tout k (1 諒 k 諒 n ) et tout sous-ensemble (i ¹, i ², ..., i ^k ) de k indices extrait de1, 2, ..., n on ait |X^{i 1} 聆 X^{i 2} 聆 X^{i k} | 閭 k.

La condition nécessaire est tout à fait évidente, mais la condition suffisante est loin de l’être.

5. Existence et construction de modèles

Un certain nombre de modèles ont été tout particulièrement étudiés, c’est le cas des carrés latins , sans doute parce qu’un mathématicien célèbre comme Euler fit à leur sujet une conjecture malheureuse et qu’il fallut attendre 177 ans pour prouver son inexactitude. En introduisant des notions comme celle d’orthogonalité, on a pu établir des liens étroits entre les carrés latins et certaines géométries finies, ou encore avec d’autres modèles comme les blocs incomplets équilibrés , ce qui a permis souvent d’étudier le même objet avec des optiques différentes.

Un carré latin d’ordre n est une matrice carrée A = (a ^ij ), ¹ size=1^諒i , ^j size=1^諒n dont les coefficients a ^ij sont 1, 2, ... , n et dans laquelle chaque entier i apparaît une et une seule fois dans chaque ligne et chaque colonne (1 諒 i 諒 n ). Il existe naturellement un carré latin d’ordre n pour tout n 閭 1. Par exemple, la table de multiplication d’un groupe fini d’ordre n est un carré latin. En fait, un carré latin peut être considéré comme la table de multiplication d’un système algébrique dont la loi est seulement supposée simplifiable. Soit l ⁿ le nombre de carrés latins d’ordre n ; jusqu’à ce jour, on a pu déterminer les valeurs exactes de l ⁿ pour 1 諒 n 諒 8. Pour calculer l ⁸, on a dû recourir à l’usage d’ordinateurs, mais même avec ceux-ci, en l’absence de nouvelles méthodes, on ne peut espérer aller bien loin dans cette direction. En revanche, l’orthogonalité a permis de trouver des résultats plus intéressants. Soit A = (a ^ij ) et B = (b ^ij ), deux carrés latins d’ordre n ; on dit qu’ils sont orthogonaux si tous les n ² couples (a ^ij , b ^ij ), où i , j = 1, 2, ..., n , sont distincts. Par exemple, les deux carrés latins d’ordre 4 indiqués ci-dessous sont orthogonaux:

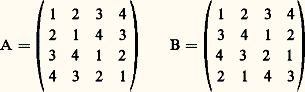Soit C la matrice ayant pour coefficients les couples (a ^ij , b ^ij ); dans C tous les n ² couples (1, 1), (1, 2), ..., (n , n ) apparaissent une et une seule fois. Dans l’exemple ci-dessus, on obtient la matrice:

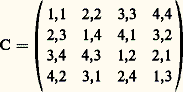On dit parfois que C est un carré gréco-latin . On s’est alors posé le problème de savoir s’il existe une paire de carrés latins orthogonaux pour tout n . Avec un peu de patience, il est facile de construire de telles paires pour n = 3, 4 et 5 et même pour des entiers supérieurs à 6. C’est Euler qui en 1782 formula ce problème en termes récréatifs. Supposons, en effet, que, dans six régiments donnés, on relève, dans chacun, six officiers, tous de grades différents, et qu’on veuille disposer ces trente-six officiers dans un carré de six cases de côté, de sorte que dans chaque ligne et dans chaque colonne il y ait un représentant de chaque régiment et un représentant de chaque grade. Une telle disposition est-elle possible? La réponse est non, et ce n’est qu’en 1900 que Tarry démontra cette impossibilité par une analyse très systématique de tous les cas possibles. Le problème des trente-six officiers était donc impossible. Si l’on numérote de 1 à 6 les six régiments et les six grades, chacun des officiers peut être repéré par un couple (i , j ), où 1 諒 i , j 諒 6; le premier indice i désigne son régiment et le second j son grade. Vouloir un représentant de chaque régiment (resp. grade) dans chaque ligne et chaque colonne et vouloir quand même disposer les trente-six officiers, c’est chercher à satisfaire aux trois exigences:

– Les premiers indices i forment un carré latin;

– Les seconds indices j forment un carré latin;

– Les deux carrés latins ainsi formés sont orthogonaux.

L’impossibilité du problème des trente-six officiers démontrée par Tarry équivaut donc à l’impossibilité de construire deux carrés latins d’ordre 6 orthogonaux. Euler n’ayant pu réussir à construire de couples de carrés latins orthogonaux d’ordre n pour des entiers de la forme n = 4 k + 2, conjectura qu’il n’existait pas de couples de carrés latins orthogonaux d’ordre n pour tout n de la forme 4 k + 2. À l’exception du seul cas n = 6, sa conjecture s’est révélée complètement erronée et, en 1959, Bose, Shrikhande et Parker démontrèrent qu’il existe en effet un couple de carrés latins orthogonaux d’ordre n pour tout n différent de 2 et 6. Avant cette date, cependant, on savait construire un couple de carrés latins orthogonaux pour tout n non congru à 2 modulo 4. Une des méthodes qui s’est révélée des plus fécondes a été de considérer pour tout n 閭 3, de la forme p ^r , où p est un nombre premier et r 礪 0, le corps fini Fⁿ ayant n éléments. Désignons par x ^o = 0, x ¹, ..., x ^n-1 les n éléments de Fⁿ et formons les matrices A¹, A², ..., A^n-1 , où A^k = (^k a ^ij ) avec ^k a ^ij , = x ^k x ⁱ + x ^j (i , j = 0, 1, ..., n 漣1; k = 1, 2, ..., n 漣1). Il est facile de vérifier que A¹, A², ..., A^n-1 sont des carrés latins orthogonaux deux à deux. On a pu étendre cette construction à tous les entiers n 令/ 2 modulo 4 et démontrer que si p ^{1r 1} p ^{2r 2} ... p ^{k r k} est la décomposition d’un entier n en facteurs premiers (les p ⁱ étant tous distincts et les r ⁱ strictement positifs) et si t = min (p ^{i r i} 漣 1) pour 1 諒 i 諒 k est supérieur ou égal à 2, alors il existe t carrés latins d’ordre n orthogonaux deux à deux.

Notons que pour n 閭 3, il est aisé de démontrer que le cardinal de tout ensemble de carrés latins orthogonaux deux à deux est au plus égal à (n 漣 1). Lorsque n est supérieur ou égal à 3 et de la forme p ^r où p est premier et r 礪 0, d’après ce qui précède, on peut construire un ensemble de carrés latins orthogonaux deux à deux qui soit de cardinal maxima, à savoir (n 漣 1). Qu’en est-il pour les autres entiers? La question est loin d’être résolue. Le théorème de Bruck-Ryser démontré en 1949 et énoncé ci-dessous apporte un premier élément de réponse. Il affirme la non-existence de certaines configurations dites plans projectifs d’ordre n , pour une famille infinie d’entiers. Sans vouloir donner de nouvelles définitions, disons que l’existence d’un plan projectif d’ordre n est équivalente à l’existence d’un ensemble de (n 漣 1) carrés latins d’ordre n orthogonaux deux à deux.

Théorème de Bruck-Ryser . Si pour n 令 1 ou 2 mod 4, il existe un nombre premier p de la forme 4 k + 3 et un entier r 礪 0 tels que p ^2r-1 divise n et p ^2r ne divise pas n , alors il n’existe pas de plan projectif d’ordre n .

Il n’y a, par exemple, pas de plan projectif d’ordre 14 et par conséquent on ne peut trouver 13 carrés latins d’ordre 14 orthogonaux deux à deux.

Donnons pour terminer un bref aperçu sur les modèles dits en blocs incomplets équilibrés. Soit X un ensemble de v éléments x ¹, x ² ..., x ^v et X¹, X², ..., X^b des sous-ensembles, dits blocs, de X qui soient distincts. On dit que ces sous-ensembles forment un modèle en blocs incomplets équilibrés de paramètres (b , v , r , k ,), si les propriétés suivantes sont vérifiées:

(I) |Xⁱ | = k pour 1 諒 i 諒 b ;

(II) tout x ⁱ 捻X appartient à exactement r blocs (1 諒 i 諒 v );

(III) toute paire d’éléments de X apparaît dans blocs.

Les paramètres b , v , r , k et ne sont pas indépendants. Il est aisé de vérifier les deux relations:

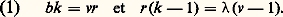Mais à leur tour, si b , v , r , k et satisfont aux relations (1), cela n’implique pas nécessairement qu’il existe un modèle en blocs incomplets équilibrés de paramètres (b , v , r , k ,). Beaucoup de résultats partiels sont connus au sujet de la construction de tels modèles. Lorsque b = v (donc k = r ), on dit que le modèle est symétrique ; on l’appelle encore (v , k ,)-configuration et l’on montre qu’un plan projectif d’ordre n est équivalent à une (v , k ,)-configuration de paramètres v = n ² + n + 1, k = n + 1 et = 1.

Encyclopédie Universelle. 2012.